Álgebra Relacional

El álgebra relacional es un conjunto de operaciones que describen paso a paso cómo computar una respuesta sobre las relaciones, tal y como éstas son definidas en el modelo relacional. Denominada de tipo procedimental, a diferencia del Cálculo relacional que es de tipo declarativo.
Tupla
Una tupla se define como una función finita que asocia unívoca mente los nombres de los atributos de una relación con los valores de una instanciación de la misma. En términos simplistas, es una fila de una tabla relacional.

Operaciones

• Selección - Restricción (σ) Esta operación selecciona un subconjunto de tuplas de una relación, todas aquellas que tengan las condiciones. Ejemplo 

• Proyección (Π) Extrae columnas de una relación, dando como resultado un subconjunto vertical de atributos de la relación. Ejemplo

• Producto Cartesiano(x) Entrega una relación, cuyo esquema contiene cada tupla de la relación A junto con la tupla de la relación B, mostrando primeramente los atributos de la relación A seguido por las tuplas de la relación B.

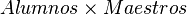
• Unión(U) es de la forma AUB Retorna el conjunto de tuplas que esten en A, o en B, o en ambas. R y S deben ser uniones compatibles(deben tener el mismo numero de columnas y el mismo tipo de dato por columna).

• Diferencia(-) es de la forma A - B Entrega todas aquellas tuplas que esten en A, pero no en B. A y B  deben ser uniones compatibles.

• División(/) Suponiendo que tenemos dos relaciones A(x,y) y B(y) donde el dominio de y en A y B, es el mismo de los dos. El operador de división A/B retorna todos los distintos valores de x tales que para todo valor y en B existe una tupla {x,y} en A.

• Agrupación (

  Ģ

  )  Permite agrupar conjuntos de valores en función de un campo determinado y hacer operaciones con otros campos. Ejemplo

Ģ _{sum(puntos) as Total Equipo} (PARTIDOS).